A scientist is studying red maple tree growth in a state park. She measured the trunk diameters of a sample of trees in the same month every other year. The tables show the data for two of the trees.

 
 

 

Multiple Choice Item: 1 point value

Question Overview:This question requires you to recognize that the tree wrap is in the shape of a cylinder without the top and bottom bases. The values for the radius and height of the t ree wrap are substituted into the formula for the surface area of a cylinder, taking care to use only the first part of the formula, which represents the area of the tree wrap. The formula requires the radius, so the diameter provided in the data table must be converted to radius before substituting. The reasoning required to solve this question is more complex than finding the area of a cylinder where the bases are present and the value of the radius is provided.

Answer Rationale:

Option A is correct. The tree wrap is in the shape of a cylinder. The area of the tree wrap is represented by the lateral area of the cylinder. The lateral surface area of a cylinder is a rectangle, where the base of the rectangle equals the circumference of the cylinder and the height of the rectangle equals the height of the cylinder. First, you must subtract the area of the two circular bases from the formula for the surface area of a cylinder. The result is the formula for lateral area of a cylinder, LA = 2nrh or LA = ndh. In the table for Tree 1, the diameter in year 13 is 22.2 inches. Using 3.14 as the value for n, you must substitute these values into the formula, which results in LA equals 2 times 22.2 times 3.14 times 45 = 3,136.86. Because tree wrap measurements are priced by the square foot, you must convert the lateral surface area from square inches to square feet. There are 144 square inches in 1 square foot; therefore, dividing the lateral area by 144 gives the lateral area in square feet: 3,136.86 divided by 144 = 22 square feet.

Option B is incorrect. If you selected t his response, you used the diameter instead of the radius when calculating the lateral area, which results in LA equals 2 times 22.2 times 3.14 times 45 = 6,273. 72, which you then converted to 44 square feet.

Option C is incorrect. If you selected t his response, you used the volume formula instead of the lateral area formula. Substituting the correct values into the volume formula yields V equals pie r squared h equals 3.14 times 11.1 squared times 45 equals 17,409.573, which you then converted Incorrect to 121 square feet.

Option D is incorrect. If you selected t his response, you divided by 12 instead of 144 when you converted from square inches to square feet.

Flag For Review

This is the flag for review button. ​ If you are not certain of an answer to a question, you can use this button to mark your answer. At the end of the test, you can to return to the question using the "Question Review Screen."
Close

Formula Sheet

Mathematics Formula Sheet

Area of a:

square A equals s squared

rectangle A equals l w

parallelogram A equals b h

triangle A equals one-half base times height

trapezoid A equals one half h times open parentheses b subscript 1 plus b subscript 2 close parentheses

circle A = pi r squared

Perimeter of a:

square P = 4 s

rectangle P = 2 l plus 2 w

triangle P = side 1 plus side 2 plus side 3

circumference of a circle C = 2 pi r OR C = pi d; pi equals approximately 3 point 1 4

Surface Area and Volume of a:

rectangular prism S A equals 2 l w plus 2 l h plus 2 w h V equals l w h

right prism S A equals p h + 2 B V equals B h

cylinder S A equals 2 pi r h plus 2 pi r squared V equals pi r squared h

pyramid S A equals one half p s + B V equals one third B H

cone S A equals pi r s plus pi r squared V equals one third pi r squared h

sphere S A equals 4 pi r squared V equals 4 thirds pi r cubed

( p = perimeter of base B ; pi is equal to approximately 3.14 )

mean

mean is equal to the total of the values of a data set, divided by the number of elements in the data set

median

median is the middle value in an odd number of ordered values of a data set, or the mean of the two middle values in an even number of ordered values in a data set

data set, or the mean of the two middle values in an even number of ordered values in a data set

Algebra

slope of a line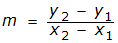 m equals the fraction, with numerator y subscript 2 minus y subscript 1 and denominator x subscript 2 minus x subscript 1

slope-intercept form

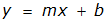of the equation of a line y equals m x plus B

point-slope form of the

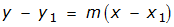equation of a line y minus y subscript 1 equals m times open parentheses x minus x subscript 1 close parentheses

standard form of a

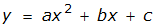quadratic equation y equals a x squared plus b x plus c

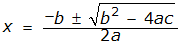quadratic formula x equals the fraction with numerator negative b plus or minus the square root of b squared minus 4 a c and denominator 2 a

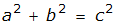Pythagorean Theorem a squared plus b squared equals c squared

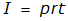simple interest I equals P r t

( I = interest, P = principal, r = rate, t = time)

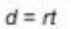distance formula d equals r t

total cost Total cost equals number of units times price per unit

Close

Calculator Reference

Calculator Reference

Basic Arithmetic

To perform basic arithmetic, enter numbers and operation symbols using the standard order of operations. The word “minus” is voiced for the operation of subtraction. The phrase “change sign” is voiced when creating a negative number. To create a negative number, enter the number first, and then press the Change Sign key.

NOTE: To complete all calculations, it is necessary to press the Enter key.

Arithmetic Example 1: Eight times open parentheses negative four close parentheses plus seven equals

The key sequence for this example is voiced by the calculator as follows:

Voiced as:

“Eight, times, four, change sign, plus, seven, enter, negative twenty-five”

The correct answer = -25

Arithmetic Example 2: Zero minus three plus open parentheses negative three close parentheses plus four minus open parentheses negative four close parentheses equals

Voiced as:

“Zero, minus, three, plus, three, change sign, plus, four, minus, four, change sign, enter, two”

The correct answer = 2

Percent

To perform calculations with percent, enter the base number, then use the Percent key.

Percent example: 40 x 560 =

Voiced as:

“Five, six, zero, times, four, zero, percent, enter, two hundred twenty-four”

The correct answer = 224

Scientific Notation

To perform calculations with scientific notation, use the Scientific Notation key. To create a number in scientific notation format, enter the base number. Use the Change Sign key to change the sign if necessary. Press the Scientific Notation key and then enter the numerical exponent. Use the Change Sign key to change the sign of the exponent if necessary.

The answer to calculations involving scientific notation will be given in standard numerical format.

Scientific Notation example: Seven point eight times ten to the eight power minus 1.5 times ten to the eight power equals

Voiced as:

“Seven, point, eight, times ten power, eight, minus, one, point, five, times ten power, eight, enter, six hundred thirty million”

The correct answer = 630000000

Fractions and Mixed Numbers

To perform calculations with fractions and mixed numbers, use the 2nd Function key, followed by the Fraction key. To create a fraction or mixed number, press the 2nd Function key, followed by the Fraction key. The Open Bracket key will automatically appear. Next, enter a whole number (use zero for simple fractions), then press the Comma key. Next, enter the numerator, press the Division key, enter the denominator, and then press the Close Bracket key. The answers to calculations involving fractions and mixed numbers will automatically be formatted in reduced form.

Fraction example: Two ninths times three sevenths equals

Voiced as:

“Second, fraction open bracket, zero, comma, two, divide by, nine, close bracket, times, second, fraction open bracket, zero, comma, three, divide by, seven, close bracket, enter, 2 over 21”

The correct answer = 2/21

Mixed Numbers example: twelve and five sixths minus one and one half equals

Voiced as:

“Second, fraction open bracket, one, two, comma, five, divide by, six, close bracket, minus, second, fraction open bracket, one, comma, one, divide by, two, close bracket, enter, eleven and one-third”

The correct answer = 11 1/3

Powers and Roots

To calculate the square of a number, use the X-Squared / Square Root key. Enter the number, then the X-Squared / Square Root key, then press the Enter key.

Squares example: One point two squared

Voiced as:

“One, point, two, x-squared, enter, one point four four”

The correct answer = 1.44

Powers Other than 2

To calculate powers other than two, use the Power / Nth-Root key. Enter the base number and press the Power / Nth-Root key. Then enter the exponent and press the Enter key

Powers Other than 2 example: Seven to the fourth power equals

Voiced as:

“Seven, power, four, enter, two thousand four hundred one”

The correct answer = 2401

Square Roots

To calculate square roots, use the 2nd Function key and X-Squared / Square Root key. Press the 2nd Function key, and then the X-Squared / Square Root key, followed by the number, then the Enter key.

Square Roots example: Square root of five hundred twenty nine

Voiced as:

“Second, square root of, five, two, nine, enter, twenty-three”

The correct answer = 23

Non-Square Roots

To calculate roots other than square roots, use the 2nd Function key and Y-Power-X / X-Root-Y key. First, enter the numerical root, followed by the 2nd Function key. Then press the Y-Power-X / X-Root-Y key, enter the base number, and press the Enter key.

Non-Square Roots example: Cube root of one thousand seven hundred twenty eight equals

Voiced as:

“Three, second, y-root, one, seven, two, eight, enter, twelve”

The correct answer = 12
Close